dCS APEX Ring DAC

Oryginalny tekst artykułu w języku angielskim znajduje się tutaj

Część 1: Podstawy kodowania PCM

Aby opisać, jak działa Ring DAC - i każdy DAC - należy zacząć od samych podstaw cyfrowego audio z perspektywy kodowania PCM [Pulse Code Modulation]. Każdy zgodzi się bowiem, że to dominujący format cyfrowego zapisu danych audio.

Dźwięk jest analogowy. Powstaje, kiedy zmiany ciśnienia wpływają na cząsteczki gazów, z których składa się powietrze, w efekcie czego cząsteczki te uderzają o siebie generując falę podłużną. Wyobraźmy sobie dwóch ludzi, którzy trzymają rozciągniętą między nimi długą sprężynę. Kiedy jeden z  nich popchnie nagle jej koniec, powstaje drobna ’zmarszczką’, która przesuwa się wzdłuż sprężyny: jej zwoje sukcesywnie zbliżają się do siebie a następnie oddalają.

To samo dzieje się z dźwiękiem. Kiedy ktoś mówi, jego struny głosowe drżą i poruszają do przodu i do tyłu cząsteczki gazu znajdujące się blisko nich. W ten sposób powstaje dźwiękowa fala podłużna rozchodząca się w powietrzu. Kiedy fala ta dociera do ludzkiego ucha, zmiany ciśnienia powietrza zamieniane są w sygnał elektryczny docierający do mózgu, który odbierany jest przez słuchacza jako dźwięk.

Nagrywanie dźwięku polega na jak najdokładniejszym zapisaniu tych zmian ciśnienia powietrza w sposób, który umożliwi ich późniejsze odtworzenie przez głośniki obecne w słuchawkach i kolumnach, co pozwoli słuchaczom usłyszeć, jak brzmiało zarejestrowane wydarzenie muzyczne.

W dzisiejszym świecie, najczęściej nagrywa się występy muzyków za pomocą jednego lub wielu mikrofonów [zamieniających kinetyczną energię cząsteczek w energię elektryczną] oraz przetwornika analogowo-cyfrowego [Analogue to Digital Converter, ADC] zamieniającego zmienne napięcie prądu w cyfrowe dane, które mogą następnie być zapisane w pamięciach komputerowych, przesłane przez internet, itd.

Przetwornik ADC ocenia zmiany napięcia prądu, który dociera z mikrofonu lub konsoli mikserskiej i zapisuje je w postaci grup składających się z dwóch cyfr [1 i 2] nazywanych ’słowami’. To są dwie najważniejsze zmienne formatu PCM: częstotliwość próbkowania [jak często oceniane jest napięcie i zapisywane próbki] oraz głębia bitowa nazywana też długością słowa lub rozdzielczością [jak wiele bitów - jedynek i zer - są w każdym zapisanym słowie].

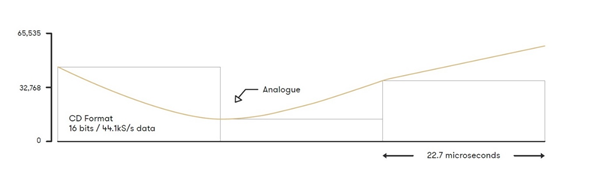
Wykres przedstawia w jaki sposób analogowa fala dźwiękowa może zostać oddana w cyfrowym zapisie PCM z głębią 16 bitów i próbkowaniem 44 100 razy na sekundę.

Głębia bitowa

Wiele urządzeń cyfrowych, w tym odtwarzacze płyt CD, wykorzystuje słowa długości 16 bitów. Oznacza to, że ADC może zapisać wartość napięcia próbki na jednym spośród 65535 możliwych poziomów. Długość słowa, czyli głębia bitowa, określa jak wiele bitów można wykorzystać do zapisania absolutnej pozycji fali dźwiękowej w cyfrowym nagraniu audio. Uważa się, że ludzkie ucho może odbierać nagrania o 20-bitowym zakresie dynamiki, co równa się około 140 dB [górną granicę wyznacza próg bólu]. Na 16-bitowych płytach CD można zapisać zakres dynamiki wynoszący 96dB [czyli różnicę między najcichszym a najgłośniejszym próbkowanym dźwiękiem]. Choć zastosowanie dithera oraz dodanie do sygnału niewielkiego szumu, może zwiększyć zakres dynamiki do 120dB, co jest znaczącą poprawą. Formaty wysokiej rozdzielczości, np. 24-bity, pozwalają osiągnąć zakres dynamiki na poziomie 144dB. Zakładając, że sprzęt naprawdę pozwala na pracę z zapisem 24-bitowym.

Często spotykanym błędem jest założenie, że format 24-bitowy pozwala zapisać dźwięki cichsze i głośniejsze niż format 16-bitowy. Nie oto jednak chodzi. Próbkowaniu poddawane są dźwięki o tym samym zakresie głośności, ale sampling [czyli próbkowanie] 24-bitowy może zapisać te dźwięki ze znacznie większą ilością stopni niż 16-bitowy. Oznacza to, że absolutna wartość fali dźwięku w danym miejscu może być zapisana dużo dokładniej.

Wyobraźmy sobie, że próbujemy zmierzyć wysokość konkretnego okna w wieżowcu a nasze narzędzia mogą mierzyć jedynie z dokładnością 1m. Okno ma w rzeczywistości 10,7m. Można więc uzyskać pomiar 10 lub 11m. Każda z wartości obarczona jest błędem.

Wyobraźmy sobie następnie dokonywanie pomiaru tego samego okna za pomocą narzędzia o dokładności 0,2m. Nadal nie da się uzyskać dokładnego wyniku pomiaru wysokości okna, ale możliwość określenia wartości 10,6 lub 10,8m daje wynik dużo bliższy rzeczywistości.

Dokładnie to samo dzieje się podczas zwiększania głębi bitowej w zapisie cyfrowego audio. Jesteśmy w stanie określić rzeczywistą wartość fali dźwiękowej z dużo większą precyzją, co redukuje tzw. szum kwantyzacji, który jest słyszalnym szumem wynikającym z błędów pomiaru.

Kiedy określasz, że  okno wysokości 10,7m  ma wysokość 11m, te 30cm błędu w wyniku pomiaru daje negatywny efekt słyszalny w zapisie audio.

Podczas pracy z audio wysokiej rozdzielczości, każdy bit dodany do głębi bitowej zmniejsza błąd kwantyzacji o połowę, zmniejsza siłę błędu cztery razy, przez co redukuje poziom szumu kwantyzacji o 6dB. 

Częstotliwość próbkowania

Skoro człowiek słyszy jedynie częstotliwości poniżej 20 000Hz, czy jest sens stosowania częstotliwości próbkowania wyższej niż 20 000Hz? Okazuje się, że tak. Jednym z najważniejszych aspektów cyfrowego audio jest tzw. prawo Nyquista, według którego cyfrowe próbki muszą być określane z częstotliwością co najmniej dwa razy wyższą niż najwyższa częstotliwość dźwięku jaką zamierza się zarejestrować. Jako, że człowiek słyszy do około 20 000 Hz, aby odtworzyć  pełen zakres słyszanych dźwięków częstotliwość cyfrowego próbkowania musi wynosić co najmniej 40 000 Hz. Ze względów, które omówimy później [związanych z filtrowaniem we wnętrzu przetwornika cyfrowo-analogowego], częstotliwość próbkowania jest zwykle nieco wyższa. W przypadku płyt CD jest to 44 100 Hz. Częstotliwość próbkowania określa ile razy na sekundę ’pobierana’ jest cyfrowa próbka, czyli określana jest wysokość fali akustycznej.

Co więcej, wyższe częstotliwości próbkowania pozwalają na zastosowanie delikatniej działających filtrów antyaliasingowych, które ’wygładzają’ schodkowy  kształt odtworzonej fali dźwiękowej [filtry cyfrowe, z racji swego olbrzymiego znaczenia zostaną dokładnie omówione w dalszych artykułach]. W skrócie - im wyższa częstość próbkowania i delikatniejszy filtr, tym mniejszy wpływ samego filtra na sygnał audio i mniejsza ilość efektów ubocznych działania filtra [na przykład tzw. dzwonienia].

Częstotliwość próbkowania i głębia bitowa to dwie wartości definiujące format PCM. Na wyświetlaczach komponentów dCS widoczne są dane dotyczące  odtwarzanych plików PCM, na przykład 24/192, kiedy plik ma głębię 24-bity i częstość próbkowania 192kHz.

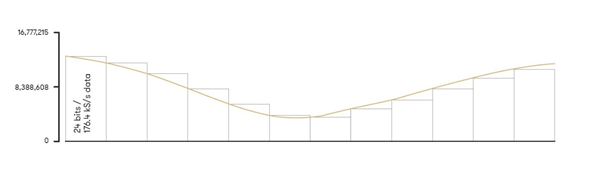
Ten wykres przedstawia w jaki sposób analogowa fala dźwiękowa może zostać oddana w cyfrowym zapisie PCM z głębią 24 bitów i próbkowaniem 176 400 razy na sekundę. Wyższa, niż dla CD, częstość próbkowania pozwala uzyskać znacznie większą dokładność na osi X wykresu a większa głębia bitowa umożliwia dużo dokładniejsze odwzorowanie przez każdą z próbek amplitudy fali dźwiękowej - na osi Y wykresu

Skoro poznaliśmy podstawy kodowania PCM, przejdźmy do następnego popularnego formatu, PDM [Pulse Density Modulation] będącego podstawą zapisu DSD. Potem zaś zajmiemy się konwersją cyfrowo-analogową.

Część 2: Podstawy kodowania Pulse Density Modulation [modulacja gęstości impulsów, DSD]

W przeciwieństwie do kodowania PCM, w którego przypadku proces samplowania w konwerterze analogowo-cyfrowym dotyczy wartości napięcia docierającego sygnału, kodowanie PDM określa oparciu czas dzielący dwie próbki, co pozwala ocenić czy poziom sygnału rośnie, czy maleje. Jeżeli dwie kolejne próbki są bliżej siebie - amplituda fali rośnie. Jeżeli próbki są dalej od siebie - amplituda fali zmniejsza się. Pojedyncza próbka nie pozwala na ocenę absolutnej wysokości fali [jak to jest możliwe w przypadku PCM], ale zestawione razem próbki dają dokładne odwzorowanie rzeczywistej fali dźwiękowej.

Wadą tej metody jest niewiarygodnie niska ’rozdzielczość dynamiczna’ [ilość informacji na temat amplitudy zawartej w każdej z próbek] wynosząca jedynie 1 bit. Próbki muszą więc być pobierane ze znacznie większą częstotliwością niż w przypadku formatu PCM. Najczęściej zapis PCM opiera się na próbkowaniu 44 100 razy na sekundę. Zapis DSD wymaga częstości co najmniej 64 razy większej, około 2 800 000 próbek na sekundę.

Ten proces zapisu cyfrowego audio generuje dużo większy szum. Wynika to zarówno z niskiej głębi bitowej [przy 1 bicie powstaje znacznie więcej szumu kwantyzacji] oraz większej częstości próbkowania [zgodnie z ogólną zasadą, że zwiększanie częstości włączania i wyłączania urządzeń generuje szum]. Aby format ten był użyteczny, dane są poddane procesowi, który przenosi szum kwantyzacji w rejon ultrasoniczny [powyżej 20kHz], gdzie staje się niesłyszalny.

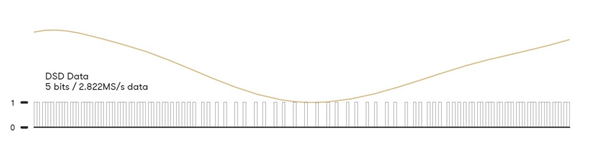
Rezultatem jest praktycznie 24-bitowa rozdzielczość w zakresie pasma słyszalnego [0Hz - 20kHz] i rozciągnięcie przenoszonego pasma powyżej 100kHz. Skutkiem  podejścia 1-bitowego jest duża ilość szumu ultrasonicznego [w zakresie 20kHz - 1,4MHz], ale nie jest on zwykle słyszalny jako szum tła. Ta metoda cyfrowego kodowania muzyki stosowana jest w formacie Direct Digital Stream [DSD]. Zaś format 1-bitowej konwersji jest podstawą działania konwerterów cyfrowo-analogowych delta-sigma strumienia bitów [które zostaną omówione dalej].

Zapis DSD jest rozwijany poprzez zwiększenie częstotliwości próbkowania. Pierwotny format, określany jako DSD64, opierał się na próbkowaniu z częstością 64 razy większą niż dla płyt CD. Format DSD128 to częstość 128 razy większa niż dla CD. Potem zaś pojawiły się formaty DSD256 i DSD512 z odpowiednio większymi częstościami próbkowania.

Pliki DSD, nawet w standardowym formacie DSD64, są duże. Dla dwukanałowego stereo tempo przesyłu danych wynosi 5644,8 kb/sek.

Ten artykuł nie jest zbyt długi. Ale dopiero po omówieniu podstawowych formatów, możemy zająć się naprawdę ciekawymi rzeczami. Następnym tematem są podstawy konwersji cyfrowo-analogowej. Zaczniemy od drabinki rezystorowej. 

Część 3: Wstęp do konwersji cyfrowo-analogowej

DAC [digital to analogue converter], czyli konwerter cyfrowo-analogowy, w takiej lub innej formie, jest podstawowym elementem każdego współczesnego systemu audio. Odgrywa kluczową rolę w przekładzie zapisanego wystąpienia artysty na muzyczne przeżycia będące udziałem słuchacza. Podstawowym zadaniem konwertera jest tłumaczenie cyfrowych plików - zapisanych na płytach CD,  w pamięci, na dyskach sieciowych lub dostępnych w serwisach streamingowych - na zmiany [analogowego] napięcia prądu napędzającego głośniki.

Podczas konwersji cyfrowo-analogowej, należy zwrócić uwagę na dwie kwestie: czy konwerter jest w stanie prawidłowo odtworzyć amplitudę zarejestrowanej fali [innymi słowy, czy potrafi generować odpowiednie napięcie] oraz czy potrafi zrobić to w odpowiednim momencie? Zdolność do generowania odpowiedniego napięcia zależy od budowy samego konwertera. Umiejętność konwersji próbki w odpowiedniej chwili zależy od taktowania całego systemu. Najpierw omówię budowę konwerterów, zaś synchronizacja i taktowanie w cyfrowym audio zostanie omówiona w następnej kolejności.

Cyfrowe dane audio zapisane są w postaci dwójkowej, jako zera i jedynki ułożone w serie ’próbek’. Ilość znaków w próbce, która reprezentuje wyjściową falę dźwiękową, nazywana jest głębią bitową. I tak: w 16-bitowym zapisie audio, każda próbka składa się z 16 znaków [z których każdy może być zerem lub jedynką]. DAC musi je przełożyć na napięcie prądu, który służy następnie do napędzenia głośników w słuchawkach lub kolumnach. Wykorzystuje się do tego układy źródeł prądowych: komponentów elektronicznych, z których każdy generuje określone napięcie.

Jednym z najczęściej wykorzystywanych sposobów konwersji D/A jest posiadanie jednego źródła prądowego przypisanego jednemu z bitów sygnału audio. Na przykład: jedno źródło prądowe zawsze oddaje status pierwszego bita próbki, kolejne źródło oddaje status drugiego bita, następne - trzeciego bita, itd. Wraz ze wzrostem liczby źródeł prądowych, ilość energii jaką każde z nich musi wytworzyć zmniejsza się [o połowę dla każdego następnego źródła].

Na schemacie, taki układ elementów wygląda jak drabina. Stąd wzięła się nieformalna nazwa grupy tak zbudowanego przetwornika: mówi się o nim Ladder DAC, czyli przetwornik drabinkowy. Aby zapewnić spadek napięcia generowanego przez każde kolejne źródło prądowe znajdujące się układzie, między kolejnymi źródłami muszą znajdować się rezystory. W zależności od sposobu ich rozmieszczenia, przetworniki drabinkowe dzielą się na dwie główne grupy: przetworniki R-2R i przetworniki ważone binarnie.

Ważna uwaga: DAC stosowany w urządzeniach dCS [Ring DAC] nie jest przetwornikiem drabinkowym. Różnica zostanie omówiona poniżej.

DAC R2R

Konwerter tego rodzaju do kontroli napięcia generowanego przez każde ze źródeł prądowych wykorzystuje rezystory o dwóch wartościach. Rezystory o wartości R znajdują się między poszczególnymi sekcjami źródeł prądowych. W obrębie samych źródeł prądowych znajdują się zaś rezystory wartości 2R. Jeżeli konkretny bit w sygnale audio ma wartość wysoką [1 zamiast 0], zamyka się odpowiadająca mu bramka i źródło  zaczyna generować prąd. Prąd ze wszystkich źródeł trafia do wspólnej magistrali, gdzie jest sumowany - tak powstaje końcowy sygnał wyjściowy z przetwornika.

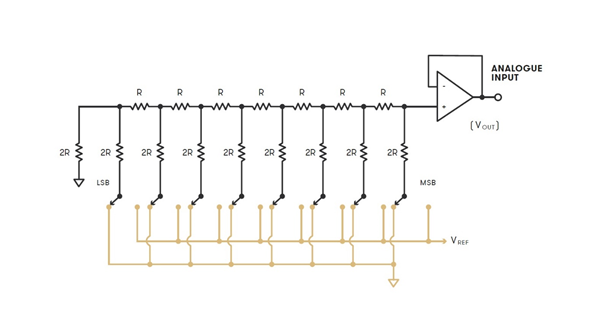
DAC ważony binarnie

W konwerterze tego rodzaju wykorzystuje się rezystory o zmniejszających się wartościach, co pozwala osiągnąć zwiększającą się różnicę mocy generowanej przez źródła prądowe. Jeżeli pierwszy rezystor ma wartość R, następny będzie mieć 2R, kolejny 4R, 8R, itd. - w zależności od ilości wymaganych kroków.

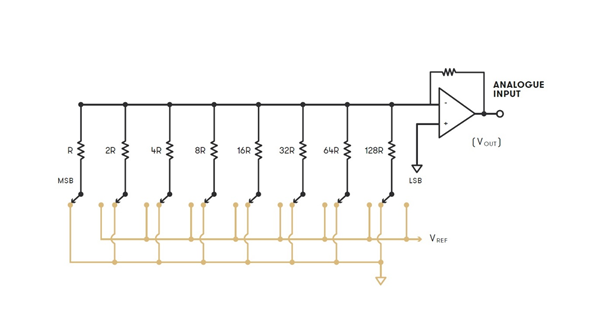
Główna wada opisanych powyżej konstrukcji wynika z faktu, że poszczególne rezystory o teoretycznie tych samych wartościach [jak wszystkie komponenty elektroniczne] różnią się od siebie. Oporność Rezystory wyprodukowane z najwyższą możliwą dokładnością mogą różnić się od nominalnej wartości o +/- 2,5%. Oznacza to, że prąd generowany  przetworniku drabinkowym może być wyższy lub niższy niż trzeba. Zakładając, że to samo źródło prądowe przetwornika jest zawsze wykorzystywane dla konkretnego bitu w sygnale audio, błąd jest dokładnie taki sam, kiedy bit ten ma wartość 1. W ten sposób różnice rezystancji komponentów układu są związane z obróbką sygnału audio. Ich rezultatem są słyszalne zniekształcenia oraz niepożądane komponenty harmoniczne.

Warto też podkreślić, że najważniejsze źródła prądowe [odpowiadające najważniejszym bitom sygnału audio] mają taki sam margines błędu jak źródła najmniej ważne. W przypadku 24-bitowego przetwornika drabinkowego, wynoszący 1% błąd dotyczący najważniejszego bita [MSB, most significant bit, największe źródło prądowe] będzie większy od całego 7 bita i 104dB głośniejszy niż bit 24-ty. Aby osiągnąć rzeczywistą rozdzielczość 24-bitową, MSB musi osiągnąć dokładność na poziomie 0,000006%.

Kolejnym problemem przetworników drabinkowych są tzw. zniekształcenia przejścia przez zero. Zakładając, że z każdym źródłem prądowym związana jest możliwość wystąpienia określonego błędu, zastanówmy się, co dzieje się w 16-bitowym przetworniku, kiedy amplituda reprodukowanego sygnału zmienia się z 32767 na 32768? Z pozycji, w której pierwszy [najważniejszy] bit ma wartość 0 a pozostałe 15 bitów ma wartość 1, DAC przechodzi w stan,  w którym pierwszy bit ma wartość 1 a pozostałe 15 ma wartość 0. Nazywamy to punktem przejścia przez zero. Wielkość błędów związanych z każdym źródłem prądowym/bitem - zwłaszcza, że zestawiamy sumę 15 błędów dla pozycji 32767 z jednym błędem dla 32768 - jest bardzo duża w porównaniu z najmniej istotnym bitem [LSB]. Oznacza to, że zmiana z 32767 na 32768 w przetworniku może być dużo większa niż LSB. Rezultatem tego są zniekształcenia liniowe, ekstremalnie niepożądane.

Aby uniknąć problemów związanych z generowaniem zniekształceń liniowych w przetwornikach drabinkowych, dla określonych wartości próbek najlepiej usunąć połączenie między oryginalnym sygnałem a błędami wynikającymi z różnic fizycznych parametrów rezystorów. Jak to osiągnąć wytłumaczymy w następnym artykule, w którym przedstawiona zostanie architektura przetwornika Ring DAC opracowanego przez firmę dCS.

Część 4: Ring DAC

W jaki sposób można poradzić sobie z opisanymi powyżej problemami przetworników drabinkowych? Jak może wyglądać DAC zaprojektowany od podstaw pod kątem efektywnego korygowania błędów konwersji i usuwania zniekształceń? Teraz właśnie do gry wchodzi Ring DAC.

Ring DAC to opracowana przez firmę dCS technika konwersji cyfrowo-analogowej, która jest stosowana we wszystkich komponentach firmy. Na pierwszy rzut oka, układ przetwornika Ring DAC wygląda podobnie jak przetworniki drabinkowe. Każde źródło prądowe i tu jest związane z systemem rezystorów a prąd trafia do wspólnej magistrali sumującej. Ring DAC różni od przetworników drabinkowych przede wszystkim przez fakt, że obecne w nim źródła prądowe mają takie samo znaczenie. Dlatego czasem jego architektura jest nazywana ’unitarnie ważoną’. Poza tym, Ring DAC nie wykorzystuje za każdym razem tego samego źródła prądowego dla tego samego bita. W jego obrębie znajduje się 48 źródeł prądowych. Każde z nich generuje taki sam prąd. Układ programowalnych bramek FPGA sterujący pracą przetwornika pozwala włączać i wyłącza źródła prądowe w taki sposób, że podczas pracy wszystkie błędy wynikające z niewłaściwej rezystancji komponentów są uśredniane. Ten sam bit konwertowany przez Ring DAC może dać trzy różne wartości prądu - niższą, średnią i wyższą - w przeciwieństwie do przetwornika drabinkowego, gdzie prąd zawsze będzie miał taką samą wartość - niższą, średnią lub wyższą.

Opracowanie optymalnego systemu pracy przetwornika Ring DAC kosztowało sporo pracy.  Jego zaletą jest praktycznie całkowite wyeliminowanie zniekształceń liniowych, które są wyjątkowo dobrze słyszalne i odbierane jako wysoce degradujące jakość brzmienia.

Zachodzący w obrębie przetwornika Ring DAC proces można nazwać deko relacją błędów. Szum tła [błąd nieskorelowany - niezwiązany bezpośrednio z sygnałem audio] jest odbierany jako PREVALENT. Dystorsja [błąd skorelowany] taka nie jest.

W rezultacie, Ring DAC osiąga najniższy w klasie poziom zniekształceń - zwłaszcza przy niskich poziomach sygnału - dzięki czemu możliwe jest usłyszenie większej ilości drobnych detali.

Decyzja o tym, które źródło prądowe ma zostać włączone lub wyłączone w danej chwili aby osiągnąć jak najlepszy sygnał zależy od zaawansowanego zestawu zasad zapisanych w części układu nazywanej dCS Mapper. Choć na pierwszy rzut okaz schemat włączania i wyłączania źródeł prądowych wydaje się być dziełem przypadku, jest kulminacją trzydziestu lat ciągłej pracy. Opracowany zestaw wzorów, poprzez uśrednienie wpływu poszczególnych komponentów  [których parametry mogą się również zmieniać wraz z upływem czasu], umożliwia zmniejszenie poziomu szumu, zniekształceń i przesłuchów między kanałami oraz utrzymanie najwyższej możliwej liniowości odwzorowania. Nieustające prace nad udoskonaleniem Mappera pozwoliły uzyskać zmniejszenie poziomu szumu przy jednoczesnym zachowaniu liniowości brzmienia charakterystycznej dla Ring DAC. To właśnie Mapper pozwala przenieść generowany przez Ring DAC poza pasmo słyszalne, skąd może być następnie odfiltrowany.

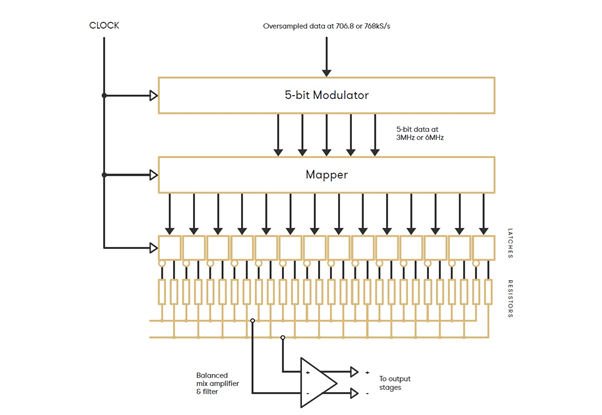
Oto schemat układu przetwornika Ring DAC

Mapper pracuje z głębią 5-bitową, dane PSC które trafiają do przetwornika Ring DAC są więc najpierw poddane overasamplingowi do 706,8 lub 768kHz. Potem zaś poddane modulacji do 5-bitów z częstością od 2,822MHz do 6,144MHz [w zależności od urządzenia, ustawień i częstości próbkowania plików ze słuchaną muzyką] a następnie docierają do Mappera, który dystrybuuje sygnał do źródeł prądowych przetwornika.

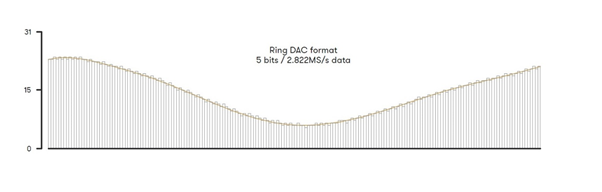
Na rysunku przedstawiono sygnał wyjściowy modulatora przetwornika Ring DAC, który zmienia sygnał wejściowy do  formatu 5-bitowego z dużą częstością próbkowania, gotowego do zamiany w postać analogową. 

Część 5: Filtry w cyfrowym audio

Producenci większości przetworników cyfrowo-analogowych podają informacje na temat stosowanych filtrów. Ponieważ filtry są wyjątkowo ważną częścią przetwornika, warto wiedzieć jak działają.

Aby zrozumieć dlaczego potrzebujemy filtrów, najlepiej zacząć od samego początku, kiedy analogowy sygnał trafia do przetwornika analogowo-cyfrowego na etapie nagrywania/edycji. To ważne, bowiem filtr wykorzystany na poziomie ADC ma takie samo znaczenie na to, co słyszymy, jak filtr obecny na poziomie DAC.

Wcześniej mówiliśmy o próbkowaniu sygnału audio na etapie ADC, kiedy to analogowe napięcie zamieniane jest w dane cyfrowe za pomocą szeregu ’próbek’. Najniższa częstotliwość próbkowania wykorzystywana w cyfrowym audio wynosi 44100 próbek na sekundę [S/s]. Wybór tej częstotliwości wynika z prawa Nyquista. Mówi ono, że w cyfrowym audio częstość próbkowania musi być co najmniej dwa razy większa on najwyższej częstotliwości dźwięku obecnej w konwertowanym utworze. Najwyższa częstotliwość obecna w próbkowanym dźwięku nazywa się ’częstotliwością Nyquista’. Ponieważ człowiek słyszy dźwięki o częstotliwości 20kHz - wymaga ona więc próbkowania z częstotliwością co najmniej 40000 S/s.

Co stanie się, kiedy w próbkowanym materiale znajdują się dźwięki, których częstotliwość przekracza granicę wyznaczoną przez częstość próbkowania [czyli między 0Hz a połową częstotliwości próbkowania]? Jeżeli tak się dzieje, częstotliwości te są ’sprowadzane’ do niższych wartości, co generuje zjawisko zwane aliasingiem. Choć brzmi to niezbyt intuicyjnie, ale jest przedstawione na poniższym rysunku.

Na poniższym rysunku przedstawiono sygnał wyjściowy modulatora przetwornika Ring DAC, który zmienia sygnał wejściowy do formatu 5-bitowego z dużą częstością próbkowania, gotowego do zamiany w postać analogową.

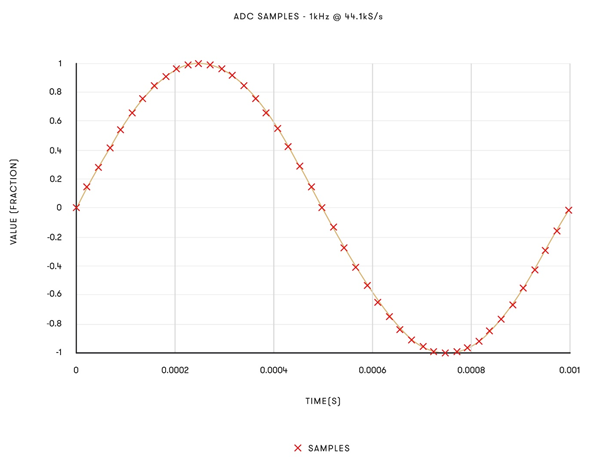
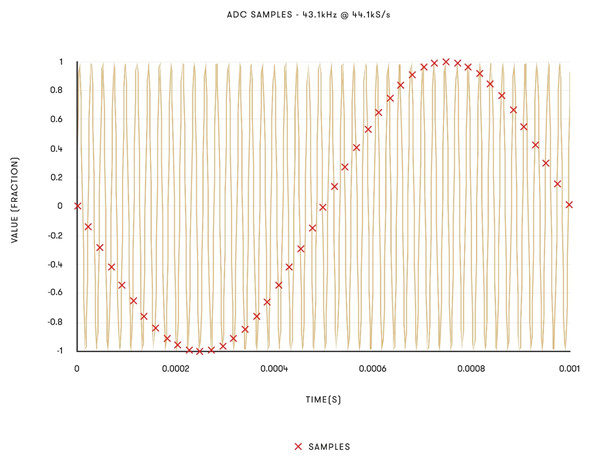
Powyższy wykres przedstawia dwa sygnały: jeden o częstości 1kHz i drugi o częstości 43,1kHz, oba próbkowane z częstotliwością 44,100 próbek na sekundę [44,1kS/s]. Sygnał 43,1kHz daje próbki, których nie da się odróżnić od próbek sygnału 1kHz [choć odwrócone w fazie]. Jeżeli więc sygnał 43,1kHz trafi do przetwornika analogowo-cyfrowego, otrzymane próbki będą takie same jak próbki sygnału częstotliwości 1kHz - w głośnikach będzie słychać ton częstości 1kHz. Oznacza to, że ADC musi usunąć wszystko, co nie mieści się w zakresie częstotliwości od 0Hz do częstotliwości Nyquista, aby nie generować błędów na etapie odtwarzania muzyki.

Za usunięcie z próbkowanego sygnału częstotliwości wyższych od częstotliwości Nyquista odpowiada filtr dolnoprzepustowy. Usuwa on wszystko, co ma częstotliwość wyższą od określonej a cały sygnał poniżej częstotliwości granicznej - przechodzi przez filtr bez żadnej zmiany. Filtr ten można zaimplementować zarówno w domenie analogowej, jak i cyfrowej.

Aby rozwiązać problem częstotliwości wyższych od częstości Nyquista, dla przetwornika analogowo-cyfrowego próbkującego z częstością 44.1kHz, oczywiste wydaje się użycie filtra, który nie działa na częstotliwości dźwięku poniżej 20000Hz a odcinającego wszystko powyżej 20001Hz. Pozwoliłby on usunąć wszystkie artefakty generowane w trakcie konwersji przy zachowaniu wierności w całym zakresie słyszalnego pasma akustycznego. A jednak, nikt nie zaleca stosowania takiego filtra.

Po pierwsze, działając w domenie cyfrowej, filtr taki wymagałby potężnej mocy obliczeniowej. Stosuje się więc filtry, które - na pewnym odcinku - obniżają amplitudę sygnału powyżej założonej częstotliwości [spadek mierzymy w decybelach na oktawę]. Ponieważ próbkowanie zachodzi z częstotliwością nieco wyższą niż dwukrotność najwyższej częstotliwości dźwięku, jaki zamierzamy zarejestrować [czyli 44100 zamiast 40000Hz], filtry mają dla siebie pewien zakres częstotliwości, w którym mogą rozwinąć swe działanie. W omawianym przypadku, filtr może pracować między 20000 a 22050Hz bez generowania błędów aliasingu i bez wpływu na częstotliwości, których człowiek usłyszeć nie może.

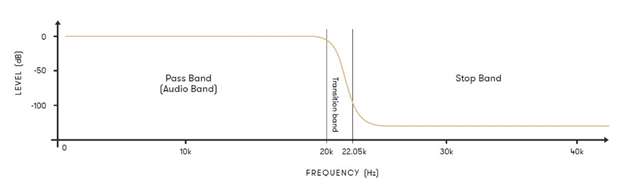
Na rysunku przedstawiono działanie filtra dolnoprzepustowego dla cyfrowego zapisu audio 44.1kHz

Oczywiście, jest to nadal niezbyt duży zakres częstotliwości dla pracy filtra. Działający w tak wąskim zakresie filtr analogowy musiałby być bardzo stromy. Jest to problemem, ponieważ filtry analogowe nie są zgodne fazowo [filtr opóźnia niektóre częstotliwości bardziej niż inne, co jest słyszalne i degraduje brzmienie], poza tym trudno uzyskać powtarzalność parametrów takiego filtra na etapie jego produkcji. Łatwo zrobić filtr analogowy dla częstości 100kHz, ale dla 20kHz sprawa jest trudniejsza. Dlatego filtry wykorzystywane do usuwania wszystkiego, co ma częstotliwość wyższą niż częstotliwość Nyquista są implementowane w domenie cyfrowej, w ramach procesora DSP.

Podczas nagrań audio, często stosuje się przetworniki ADC o dużej częstości próbkowania i prowadzi filtrowanie na granicy częstotliwości Nyquista już na poziomie strumienia danych cyfrowych. Taką metodę pracy określa się mianem ’konwersji analogowo-cyfrowej z oversamplingiem’. Na poniższym rysunku przedstawiono blokowy schemat przetwornika ADC dającego na wyjściu sygnał 16-bitów/44,1kHz.

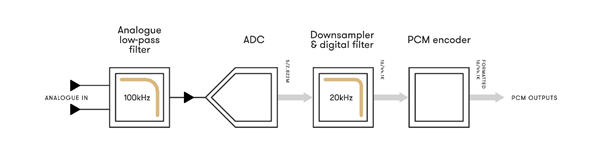Analogowy filtr dolnoprzepustowy usuwa z sygnału analogowego wszystkie częstotliwości wyższe od 100kHz, ponieważ prowadziłyby do aliasingu. Jak wspomniano powyżej, analogowe filtry działające w zakresie częstotliwości 100kz mogą być delikatne, poza tym pracują w regionach, w których nieliniowości nie mają znaczenia.

Kolejnym etapem jest konwerter analogowo-cyfrowy [ADC], który zamienia sygnał w dane cyfrowe. W konwerterze ADC firmy dCS stosowany jest Ring DAC pracujący w pętli sprzężenia zwrotnego, na jego wyjściu otrzymujemy więc dane zapisane z rozdzielczością  5 bitów i częstością próbkowania 2822000 próbek na sekundę.

Następnie dane te poddane są downsamplingowi do formatu 16-bitów/44.1kHz. Kolejnym etapem jest cyfrowy filtr usuwający wszystko powyżej 22,05kHz [częstotliwości wyższe, jeżeli ich nie odfiltrujemy, prowadzą do aliasingu]. Ostatnim etapem obróbki sygnału jest enkoder PCM formatujący dane zgodnie ze standardami S/PDIF, AES/EBU i SDIF-2.

Budowa i działanie filtra cyfrowego zastosowanego w downsamplerze również wymagają podjęcia kilku istotnych decyzji. Mówiąc najprościej, filtr cyfrowy działa poprzez przepuszczenie każdej próbki przez szereg multiplikatorów, których wspólna praca prowadzi do usunięciu z sygnału wyższych częstotliwości. Sposób ułożenia tych multiplikatorów określa się mianem ’kształtu’ filtra [filtr symetryczny lub niesymetryczny]. Filtry o różnych kształtach w różny sposób wpływają na dźwięk.

Na poniższym rysunku przedstawiono przykład działania filtra symetrycznego. Nazwano go tak, ponieważ prowadzi do powstania symetrycznego ’dzwonienia’  przed i po  impulsie poddanym obróbce. Efekt ten jest wyraźniejszy przy niższych częstościach próbkowania.

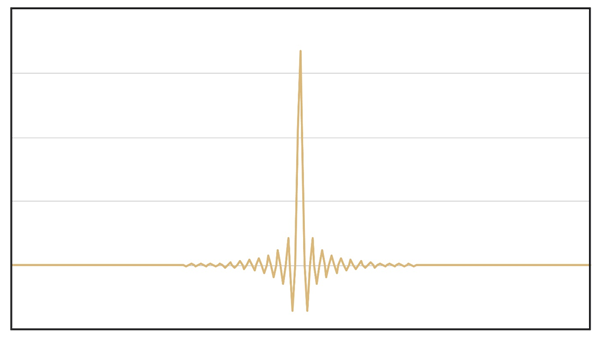
Poniższy wykres przedstawia przykład działania filtra asymetrycznego. Jego odpowiedź na sygnał jest zupełnie inna - przed impulsem nie ma żadnego dzwonienia, ale po sygnale dzwonienie jest znacznie wyraźniejsze.

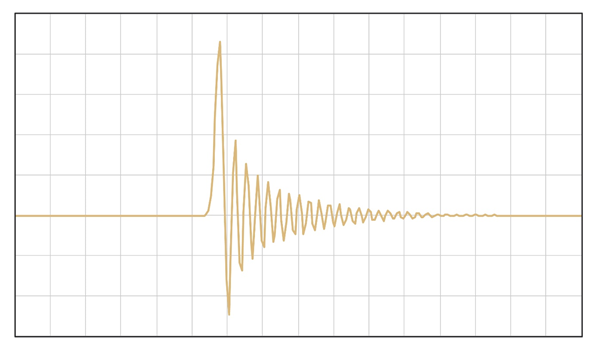
Biorąc pod uwagę, że przetwornik ADC musi stosować filtry do usuwania aliasingu i że dla częstotliwości Nyquista preferowane jest zastosowanie filtrów cyfrowych [zamiast agresywnej filtracji analogowej], należy liczyć się z obecnością dzwonienia wprowadzanego na etapie zapisu sygnału przez cyfrowe filtry w konwerterach analogowo-cyfrowych. To niezbędny kompromis i dlatego wybór filtra ma znaczenie.

Większość konwerterów ADC wykorzystuje filtry symetryczne. Oznacza to, że w cyfrowych rejestracjach dźwięku, dzwonienie będzie obecne przed i po próbkach. Należy podkreślić, że dzwonienie będzie obecne we wszystkich cyfrowych nagraniach zanim pliki trafią do przetwornika cyfrowo-analogowego. Ale to aktualnie najlepsze rozwiązanie. Zakładając oczywiście, że filtry w obrębie konwertera ADC są poprawnie zaprojektowane i zaimplementowane.

Kolejną ważną kwestią omawianego zagadnienia jest DAC, w którym cyfrowy sygnał audio zarejestrowany przez ADC zamieniany jest z powrotem w postać analogową.

Kiedy DAC rekonstruuje falę analogową z cyfrowych próbek, zachodzi zjawisko podobne do aliasingu. W związku z relacjami między częstotliwością analogowego sygnału a częstotliwością próbkowania w sygnału cyfrowego, powstają ’kopie’ konwertowanego sygnału, które są obecne wysoko w spektrum audio. Choć obrazy te istnieją poza zasięgiem ludzkiego, ich obecność może degradować dźwięk.

Z dwóch powodów. Po pierwsze: częstotliwości powyżej 20000Hz mogą wchodzić w interakcje z niższymi częstotliwościami w spektrum słyszalnym [0-20000Hz].

Po drugie: jeżeli artefakty te, zwane obrazami Nyquista, nie zostaną usunięte z sygnału audio, komponenty systemu będą próbować je odtwarzać jako wysokie częstotliwości, co stawia dodatkowe obciążenia przed głośnikami [zwłaszcza wysokotonowymi] i przed wzmacniaczami. Eliminacja obrazów Nyquista oznacza, że wzmacniacz ma więcej mocy do reprodukcji tych części sygnału audio, które chcemy słyszeć. Przynosi to ewidentne korzyści brzmieniowe.

Podobnie jak w przypadku przetworników analogowo-cyfrowych, rozwiązaniem problemów wywoływanych przez obrazy Nyquista podczas konwersji cyfrowo-analogowej jest filtrowanie - za pomocą filtra dolnoprzepustowego - wszystkiego, co znajduje się ponad najwyższą częstotliwością, którą chcemy słyszeć. Pozwala to usunąć z sygnału audio obrazy Nyquista bez wpływu na istotną dla nas muzykę. Kwestia projektu i działania tego filtra dolnoprzepustowego jest złożona i delikatna. Przede wszystkim trzeba podkreślić, że nie istnieje jedno rozwiązanie odpowiednie dla wszystkich.

Wymagania dotyczące filtra zmieniają się, oczywiście, dla plików o częstości próbkowania wyższej niż 44,1kHz [np. streaming wysokiej rozdzielczości]. Pasmo przenoszenia jest wtedy szersze, co wymusza zmiany charakterystyki filtra. W przetwornikach większości producentów znajduje się jeden zestaw filtrów w kaskadzie dla różnych częstości próbkowania. Biorąc pod uwagę zmianę wymagań wobec filtrowania przy zmianie częstotliwości próbkowania, nie jest to rozwiązanie optymalne dla high-endowych systemów.

Z tego powodu, inżynierowie dCS tworzą filtry specyficzne dla każdej częstości próbkowania. Co więcej, urządzenia dCS pozwalają na wybór jednej z kilku opcji filtrowania dla każdej częstości próbkowania. Nie ma bowiem jednego poprawnego rozwiązania w kwestii filtrowania. Wiele zależy tu bowiem od osobistych preferencji brzmieniowych słuchacza i charakterystyki odtwarzanych plików audio.

Część 6: Projektowanie filtrów dla konwerterów ADC i DAC

Jak działają filtry opisane w części 5 i jak powinno się je projektować? Choć brzmi to niezbyt intuicyjnie, filtrowanie zachodzące na poziomie ADC i DAC jest w rzeczywistości bardzo podobne.

W przetwornikach analogowo-cyfrowych, do konwersji trafia sygnał o częstości próbkowania większej niż ta, która ma znaleźć się na wyjściu [zwykle dwa razy większej]. Konwerter musi następnie usunąć wszystko powyżej częstotliwości Nyquista, co pozwala wyeliminować próbki [na przykład zmniejszając częstotliwość próbkowania z 88,2 do 44,1kHz] bez aliasingu. Odbywa się to za pomocą filtra dolnoprzepustowego w DSP.

Do przetworników cyfrowo-analogowych z oversamplingiem trafia sygnał częstotliwości próbkowania niższej niż ta, którą chcemy poddać konwersji. Istnieje wiele sposobów rozwiązania tej kwestii. Najskuteczniejszym wydaje się być dodanie próbek o zerowej amplitudzie między istniejące próbki, co zwiększa częstość próbowania a następnie usunięcie obrazów Nyquista generowanych przez ten proces. I znów, implementacja filtra dolnoprzepustowego zachodzi w DSP. 

W jaki sposób działa cyfrowy filtr dolnoprzepustowy? Mówiąc najprościej, cyfrowy sygnał przechodzi przez układ multiplikatorów, które zmieniają amplitudę próbek o pewną wartość, mieszczącą się między  0 [bez sygnału] a 1 [oryginalna pełna amplituda próbki].  Filtr opuszcza sygnał będący sumą sygnału z wszystkich multiplikatorów pomnożonych przez ich odpowiednie wartości. Każdy z multiplikatorów określany jest mianem ’tap’.

W magazynach audio często spotyka się wykresy ’odpowiedzi impulsowej’ filtrów. Przedstawiają one zazwyczaj sygnał wyjściowy filtra, który otrzymuje sekwencję próbek: najpierw o amplitudzie 0, potem o amplitudzie 1 i następnie znów o amplitudzie 0. Sekwencja ta pozwala pokazać sumaryczne działanie układu multiplikatorów, co de facto  definiuje działanie filtra. Zwykle wykres taki przypomina wykres funkcji sinc [sinus cardinalis] definiowanej jako ’sin(x)/x’ i przedstawionej na poniższym wykresie.

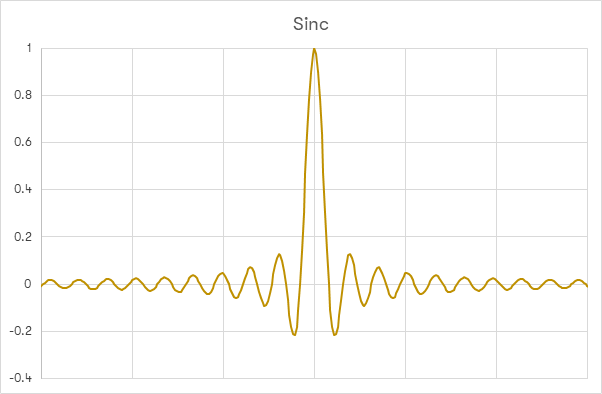
Funkcja sinc ma wiele użytecznych cech: działa jak idealny filtr dolnoprzepustowy [zestaw multiplikatorów wykorzystywanych w cyfrowych filtrach został dobrany tak, by odwzorować wykres tej funkcji - stąd wartość na osi Y jest mniejsza lub równa 1, co pokażemy poniżej]; w obu kierunkach [od impulsu] jej wykres jest lustrzanym odbiciem i ma takie samo opóźnienie dla wszystkich częstotliwości [co nie jest wspólne dla wszystkich filtrów]. Filtry analogowe opóźniają niektóre częstotliwości bardziej niż inne, przez co generują zniekształcenia fazowe. Filtry opóźniające wszystkie częstotliwości w tym samym stopniu, są określane mianem zgodnych fazowo.

Biorąc pod uwagę powyższe czynniki, funkcję sinc można modulować w celu otrzymania pożądanej odpowiedzi częstotliwościowej. Trzy najważniejsze kwestie, które trzeba uwzględnić projektując filtr cyfrowy to:

• punkt -6dB: częstotliwość, przy której filtr osiąga wzmocnienie 6dB
• długość filtra: ilość zastosowanych w filtrze multiplikatorów, z których każdy określany jest mianem ’tap’
• technika okienkowania: określana w zależności od obu powyższych kwestii [choć to bardzo uproszczone wytłumaczenie]

Częstotliwość odcięcia [punkt -6dB]

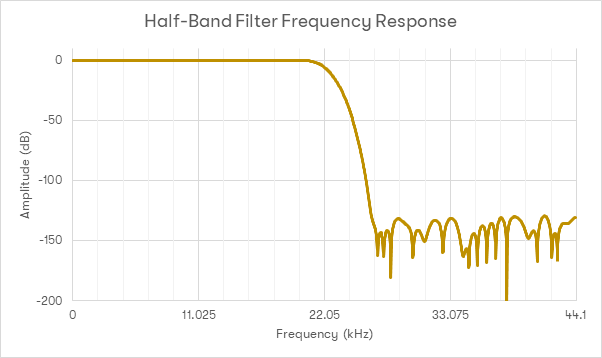
W celu zrozumienia znaczenia częstotliwości odcięcia, weźmy pod uwagę poniższy wykres przedstawiający działanie najpopularniejszego filtra. Jest to, tak zwany, filtr ’połowy-pasma’ lub ’filtr Nyquista’ z multiplikatorami opartymi o funkcję sinc. Filtr ten zaprojektowano tak, by punkt -6dB wypadał dokładnie w miejscu założonej częstotliwości Nyquista.  Dla - na przykład - filtra dolnoprzepustowego w ADC, częstotliwość Nyquista ustalono na 22,05kHz. Poniższy wykres przedstawia odpowiedź dla filtra długości 128 tapów.

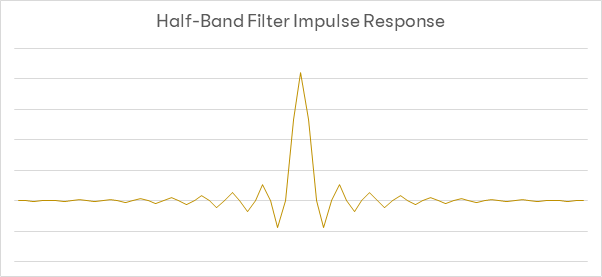
Kluczowym aspektem jest fakt, że - oprócz jednego - wszystkie pozostałe multiplikatory     mają współczynnik 0 [przedstawiono je na osi X]. Wadą filtra tego typu jest osiąganie progu 6dB dokładnie w częstotliwości Nyqyuista. Z tego powodu artefakty aliasingu z przetwornika ADC tworzące lustrzane obrazy poniżej częstości Nyquista nie będą wyeliminowane w odpowiednim stopniu. Idealny byłby filtr, który osiąga próg -6dB poniżej częstotliwości Nyqusita.

Technika okienkowania

Wykorzystanie funkcji sinc jako podstawy działania cyfrowych filtrów ma pewne wady. Po pierwsze: filtr nie może być nieskończenie długi [a sinc to przecież matematyczna funkcja bez określonej długości], rodzi to bowiem dużo problemów w realnym świecie. Wymagane są też dane z przyszłości, współczynniki multiplikatorów niosą bowiem ze sobą dane sprzed próbki, która jest właśnie odtwarzana. Jak z tego wybrnąć?

Po pierwsze, trzeba zdefiniować długość filtra. Po jej określeniu, pewna ilość próbek przychodzącego sygnału przechowywana jest w buforze. Oznacza to, że filtr może mieć dane z przyszłości dzięki opóźnieniu całości sygnału wyjściowego o kilka próbek.

Niestety, zdefiniowanie długości filtra generuje problemy natury matematycznej: wraz z oddaleniem od centralnego impulsu, uzyskane wartości stają się bardzo małe. Choć sinc    jest nieskończenie długa, ale nie jest dobrym rozwiązaniem wybieranie jej części jako podstawy do działania filtra, wycinając ’początek’ i ’koniec’ w celu uzyskania skończonej długości filtra. Powstały w wyniku tego filtr nie działa zbyt skutecznie. Na poniższym wykresie przedstawiono efekt działania filtra dolnoprzepustowego zaprojektowanego do pracy z sygnałem o częstości próbkowania 44,1kHz i długości 64 tapów, gdzie działanie funkcji sinc po prostu ucięto po zapewnieniu odpowiedniej dla działania filtra ilości współczynników.

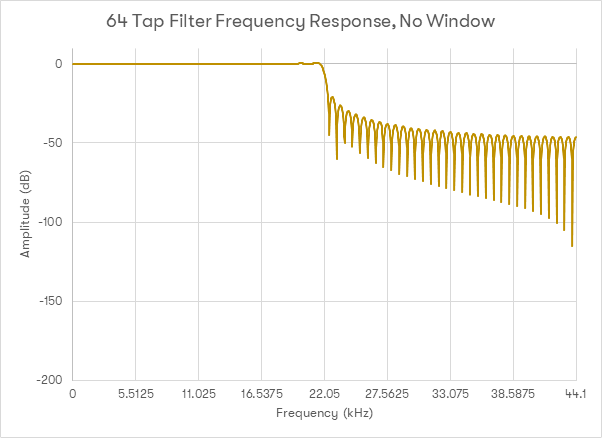
Jak widać z tego wykresu, filtr nie zapewnia dobrej odpowiedzi. Obszar usuwania częstotliwości powyżej 22,05kHz wygląda bardzo źle [zwłaszcza schodek poniżej 22,05kHz]. Problem ten najlepiej rozwiązać za pomocą techniki nazywanej ’okienkowaniem’: wybieramy zestaw współczynników, które chcemy wykorzystać [na przykład ograniczony fragment funkcji sinc] a następnie mnożymy je przez inny zestaw współczynników w celu redukcji efektów niepożądanych widocznych na powyższym wykresie.

Istnieje wiele sposobów okienkowania [różne zestawy funkcji/współczynników], ale w tym przykładzie wykorzystano okno podwyższonego cosinusa. 

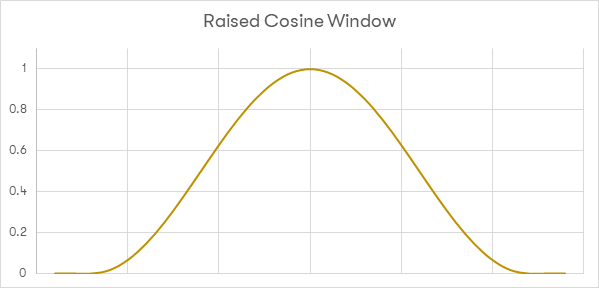
Na rysunku przedstawiono przykład okna podwyższonego cosinusa

Efekt zastosowania tej techniki w filtrze długości 64 tapów z powyższego przykładu pokazuje wykres poniżej.

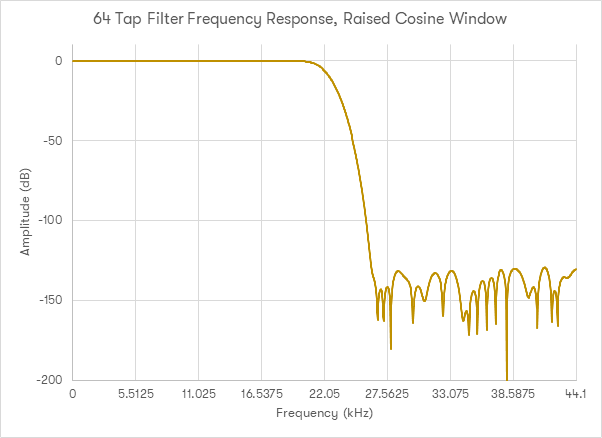
Jak widać, uzyskany efekt jest wyraźnie lepszy. Obszar usuwania częstotliwości jest teraz dużo lepszy a schodki w słyszalnym zakresie spektrum nie są teraz obecne. Przykład ten pokazuje znaczenie prawidłowego doboru sposobu okien kowania podczas projektowania filtrów dla cyfrowych układów audio.

Długość filtra

Trzecim elementem, który należy wziąć pod uwagę podczas projektowania jest długość samego filtra. Jak już wspomniano, filtr na wyjściu przetwornika cyfrowo-analogowego jest potrzebny w celu eliminacji obrazów rzekomych. Filtr ten musi jednak mieć skończoną długość - musi być dłuższy niż nic, ale nie nieskończenie długi. Jeżeli na wyjściu DAC-a nie ma filtra i próbki są odtwarzane bez zmian, rezultaty nie są idealne:

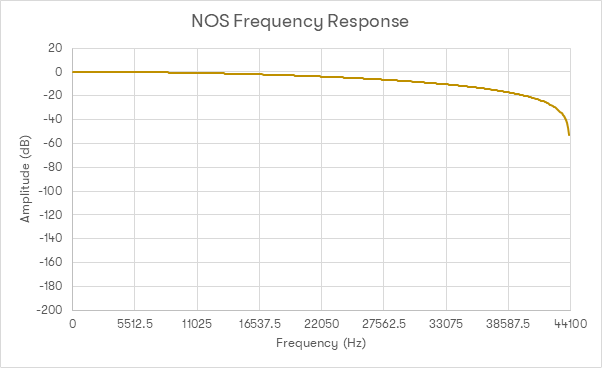
Na wykresie przedstawiono odpowiedź częstotliwościową przetwornika cyfrowo-analogowego bez oversamplingu [NOS DAC] i bez filtracji sygnału wyjściowego.

Jak wspomniano powyżej, filtr przeznaczony dla cyfrowego audio 44,1kHz nie powinien wpływać na częstotliwości poniżej 22,05kHz i powinien znacząco wyciszać wszystkie częstotliwości powyżej tego progu. Bez filtra na wyjściu, nie tylko brak wyciszenia sygnału powyżej 22,05kHz [co prowadzi do generowania dużej ilości artefaktów w zakresie wysokich tonów], ale i degradowany jest sygnał, którym jesteśmy zainteresowani: odpowiedź częstotliwościowa dla 20kHz wynosi -3dB.

Jak długi powinien więc być wiatr obecny na wyjściu przetwornika cyfrowo-analogowego? Aby pokazać znaczenie długości filtra, wykorzystamy użyty powyżej filtr Nyquista z oknem podwyższonego kosinusa. Najpierw filtr długości 32 tapów:

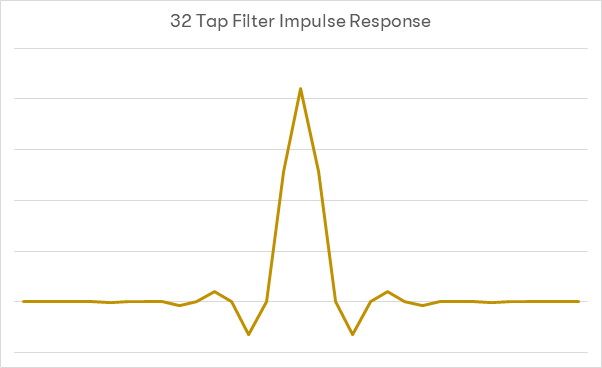
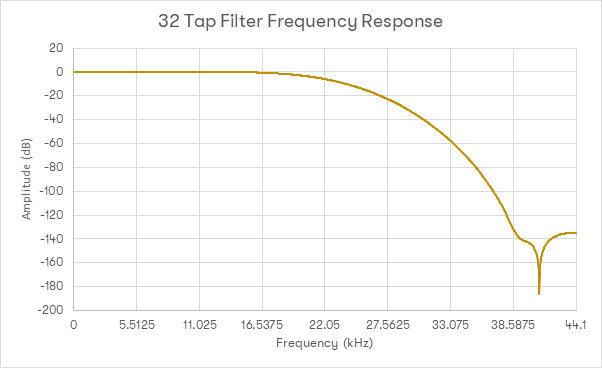
Jak widać, krzywa odpowiedzi częstotliwościowej jest nadal zbyt stroma, by korzystać z tego filtra: dla 20kHz nadal mamy około -2,8dB. Wyciszenie obrazów powyżej 33kHz [wpływających na rejon 0-11kHz]  osiąga poziom -50dB. Pasmo użytecznych częstości sięga 20kHz.

Następny przykład to ten sam filtr Nyquista z oknem podwyższonego kosinusa, ale tym raz o długości 256 tapów:

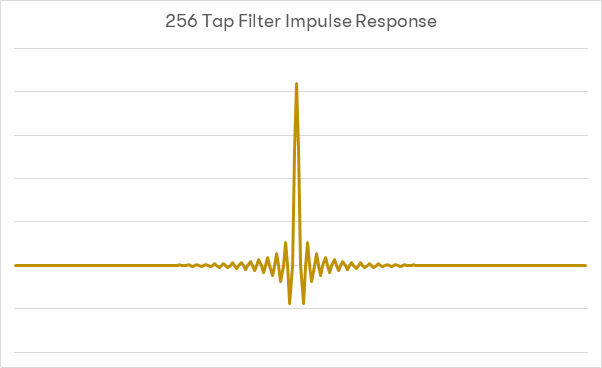
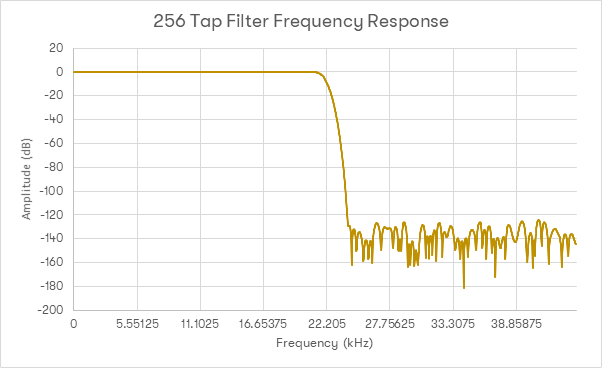
Jego odpowiedź jest wyraźnie lepsza. W słyszalnym zakresie krzywa jest płaska aż do 20kHz a pasmo wyciszania ma szerokość około 4kHz. Obrazy leżące powyżej 22,05kHz są elegancko tłumione. Wykres odpowiedzi impulsowej pokazuje jednak, że wymaganych jest dużo więcej danych sprzed aktualnie odtwarzanej próbki. W związku z tym, filtr wymaga dużo więcej próbek ’z przyszłości’, co z kolei ma wpływ na aktualną próbkę a więcej próbek ’z teraźniejszości’ będzie mieć znaczenie później.

Na końcu, ten sam filtr długości 1024 tapów:

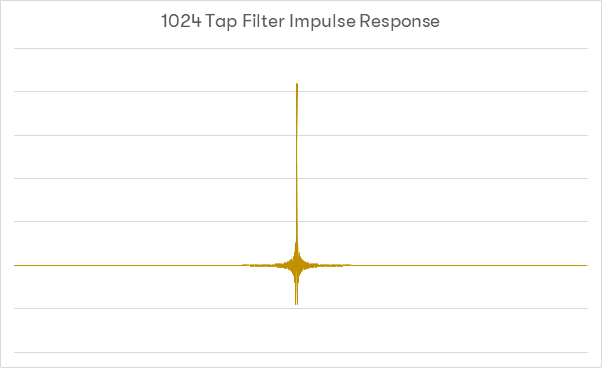
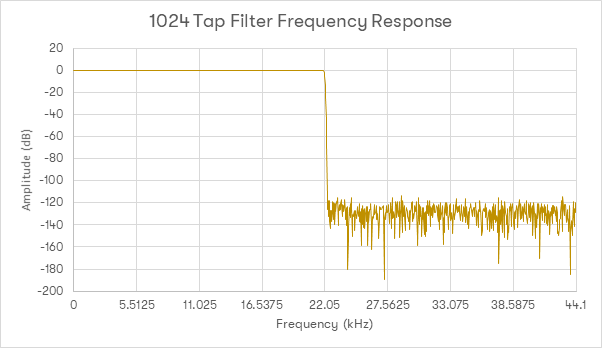
Jak widać, wydłużenie filtra wpływa na kilka kwestii. Po pierwsze: pasmo wyciszania jest  znacznie węższe, w sygnale jest więc znacznie mniej energio spoza słyszalnego pasma.    Niestety, pojawiają się również efekty niepożądane. Ponieważ wykorzystywane jest więcej multiplikatorów i więcej współczynników - w paśmie poza zakresem słyszalnym pojawia się szum [który jednak można skompensować odpowiednim okienkowaniem]. Wykorzystywane jest również znacznie więcej próbek ’z przyszłości’ [w tym przykładzie około 2014 tapów z sygnału 44,1kHz - to około 11mS] a podobna ich ilość będzie zmieniana ’w przyszłości’. Znaczenie tych czynników jest ciągle przedmiotem dyskusji, ale trzeba brać pod uwagę skąd pochodzą te próbki. 

Mając to na uwadze, pora na przykład z realnego świata…

dCS 904 - 44.1k, Filtr 1

Na wykresie przedstawiono odpowiedź częstotliwościową przetwornika dCS 904 pracującego z częstotliwością próbkowania 44,1kS/s z użyciem Filtra 1.

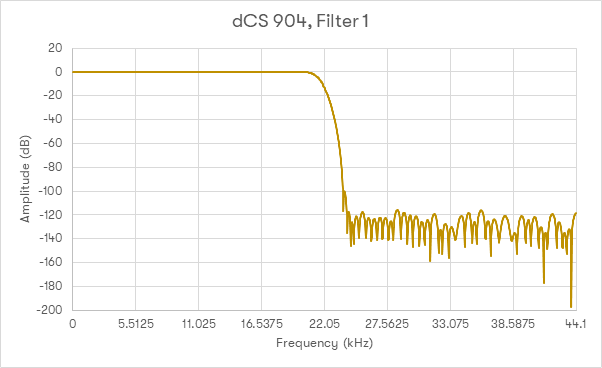
Wykres przedstawia odpowiedź częstotliwościową wszechstronnego przetwornika analogowo-cyfrowego wykorzystywanego w wielu studiach nagraniowych - modelu dCS 904. Najpierw trzeba podkreślić, że w tym przykładzie nie jest wykorzystywany filtr Nyquista stosowany w przykładach pokazanych wcześniej. Aż do częstotliwości Nyquista wzmocnienie wynosi tu 20dB. To ważne, ponieważ ADC - z definicji - ma do czynienia z sygnałami, których pasmo nie jest niczym ograniczone. Końcowy filtr ma około 100 tagów długości, co oznacza, że zastosowanie dłuższego filtra podczas odtwarzania [DAC] nie przyniesie większych korzyści. Biorąc to pod uwagę, przyjrzyjmy się kolejnemu wykresowi:

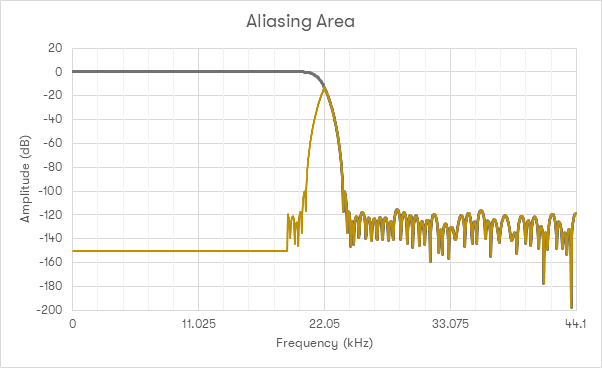
Przedstawia on obszar potencjalnych problemów wywoływanych przez ten filtr. W obszarze przejściowym, nie da się odróżnić między rzeczywistym sygnałem a aliasem. Widać więc, że stosowanie na tym etapie nadmiernie długich filtrów wymaga potem olbrzymiej pracy na poziomie DSP w celu reprodukcji czegoś, co jest faktycznie obszarem przejściowym ADC - sygnału, który nie jest pożądany i o nieznanym pochodzeniu.

Przykład ten pokazuje wyraźnie, że podczas projektowania filtrów cyfrowych należy wziąć pod uwagę cały łańcuch sygnału a nie tylko izolowany DAC. Stosowane w przetwornikach cyfrowo-analogowych filtry, które działają świetnie z realnymi przetwornikami ADC to konstrukcje idealne. W realnym świecie, jeżeli DAC nie jest wyposażony w filtr, albo jest to filtr zbyt krótki lub zbyt długi, może dojść do pogorszenia jakości brzmienia. Długość filtrów należy określić uwzględniając pozostałe istotne czynniki. Zrozumienie konieczności znalezienia kompromisowych rozwiązań pozwala stworzyć zestaw filtrów działających poprawnie niezależnie od jakości i rodzaju sygnału wejściowego. Z tego powodu przetworniki firmy dCS są wyposażone w szereg różnych filtrów do wyboru. DAC nie wie [i nie może wiedzieć] jakie filtry były użyte podczas tworzenia sygnału. To użytkownik może wybrać filtr, który zapewnia najlepsze wrażenia odsłuchowe podczas odtwarzania muzyki.

Doświadczenie zdobyte przez firmę dCS podczas tworzenia przetworników ADC i DAC pozwala na tworzenie filtrów, które osiągają najlepsze w branży rezultaty. Tak podczas testów laboratoryjnych, jak i w tracie odtwarzania muzyki w realnych systemach.

Zapraszamy do zapoznania się z kolejną częścią rozważań dotyczącą taktowania zegarowego.